

Les opérations classiques sont l'addition "+", la soustraction "-", la multiplication "*" et la division "/". A noter que le séparateur décimal est le point "." et non la virgule comme en France ! A noter ; Python interpétera un nombre avec une virgule comme un tuple, qu'on peut voir pour simplifier comme une liste de deux nombres.

Python respecte les priorités et 5x3+2 ne donnera pas le même résultat que 5x(3+2) ! A vérifier en tapant le calcul correspondant
dans la console.
Remarque : pour python tous les opérateurs doivent être écrit : si pour les mathématiciens 5(3+2) a un sens (la multiplication entre le
5 et la parenthèse est implicite) pour python cela ne veut rien dire et entrainera une erreur !
Pour la division il existe deux opérateurs donnant la partie entière du quotiont et le reste de la division euclidienne. Ces opérateurs sont respectivement "//" (division entière) et "%" (modulo). Calculer par exemple 18/5, 18//5 et 18%5.
Les puissances de 10 sont représentées par l'opérateur "e" suivant de l'exposant (entier). Cet opérateur doit forcément être précédé d'un nombre. A noter qu'un nombre écrit avec une puissance de 10 est vu par python comme un nombre à virgule (type float) et non comme un entier (type int). Cet opérateur est prioritaire sur les autres : calculer 1/2e-3 et (1/2)e-3 pour s'en assurer (attention : écrite comme cela python considèrera la puissance de 10 comme une erreur !).
Pour élever un nombre à une puissance quelconque l'opérateur à utiliser est "**". Par exemple 43 s'écrira en langage python 4**3. On pouurrait réécrire les puissances de 10 (mais je ne le conseille pas !) avec cette opérateur : 10-3 devient 10**-3 (pas besoin de parenthèses autour de -3).
L'interpréteur python ne dispose pas de fonctions mathématiques avancées comme par exemple les fonctions trigonométriques cosinus, sinus ou tangente. Il faut donc les définir en important le module math en entier ou seulement les fonctions nécessaires.
from math import *
#pour importer toutes les fonctions
from math import cos, sin, tan, radians, pi
#pour importer les fonctions cos(), sin(), tan(), radians() et la valeur de pi
Il existe d'autres façons d'importer des modules supplémentaires, mais cela change la manière d'appeler les fonctions.
import math
Il est également possible de renommer le module pour abréger son nom :
import math as m
Par exemple pour calculer le cosinus d'un angle (0 par exemple) on fera :
from math import *
cos(0)
import math
math.cos(0)
import math as m
m.cos(0)
Calculons le cosinus d'un angle droit donc 90°. Le résultat obtenu est donné en copie d'écran.
from math import cos
cos(90)
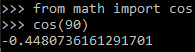
Le résultat obtenu n'est pas celui attendu car cos(90) = 0 ! La raison est toute simple : la fonction cosinus du module math prend comme argument un angle en radians et non en degrés. Il faut donc faire la conversion et le plus simple est d'utiliser la fonction radians() du module math :
from math import cos, radians
cos(radians(90))
Le résultat est très proche de 0 mais pas totalement nul. Pour avoir un résultat plus correct il faut arrondir la valeur calculée par python par la fonction round() :
round(cos(radians(90)),2) #arrondi à 2 chiffres

Dans le cas où on doive répéter plusieurs fois le même calcul, il est intéressant de savoir définir une fonction sous python qui permet de ne pas avoir à répéter le calcul.
L'écriture d'une fonction se fait toujours de la même façon (Un exemple de fonction est donnée en illustration dans Thonny):

Pour utiliser la fonction il faut d'abord l'exécuter dans l'IDE (le triangle banc dans un rond vert pour Thonny, un triangle vert dans
Pyscripter) puis taper f(2) dans la console pour calculer la valeur obtenue pour x = 2.
Il est tout à fait possible de définir une fonction dans la console : Thonny comme Pyscripter ajoutent automatiquement l'indentation. Il
faut juste appuyer deux fois sur la touche entrée à la fin de la fonction.
Pour tracer des graphiques avec python il faut utiliser un module dédié : pyplot faisant lui même partie du module matplotlib. Comme son nom est un peu long on va le renommer en plt (nom utilisé habituellement pour ce module, mais on peut en utiliser un autre...). La première ligne de code sera donc :
import matplotlib.pyplot as plt
Ensuite il faut donner les valeurs de x pour lesquels on va tracer le graphique. Ces valeurs sont données sous forme de liste entre crochets séparées par des virgules :
x=[0,1,2,3,4,5,6,7,8,9,10]
On calcule les valeurs de y correspondantes (ou on les saisit sous forme de liste si ce sont des mesures). On peut utiliser une fonction définie auparavant pour le faire.
y=[n**2+n+1 for n in x]
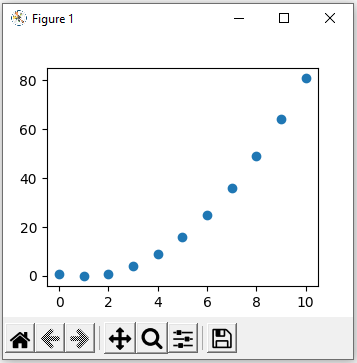
On trace les points avec la fonction scatter() :
plt.scatter(x,y)
Et on l'affiche
plt.show()
On peut préciser la couleur et la forme du marqueur en précisant marker = 'forme' et color = 'lettre' où forme et lettre peuvent être :
Le principe est le même que précédemment sauf que la fonction à utiliser est la fonction plot() du module pyplot.
plt.plot(x,y)
Et on l'affiche
plt.show()
Par défaut il n'y a pas de points de tracé mais on peut les rajouter en précisant marker = 'forme' et choisir la couleur par color = 'lettre' où forme et lettre sont définis de la même façon que précédemment. On peut également préciser le style de ligne par linestyle='style'
plt.plot(x,y,'r+-.')
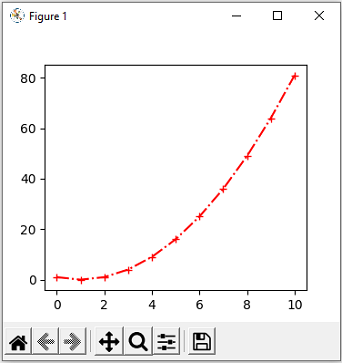
On le sait les calculs de physique (et de chimie) font intervenir des constantes, comme la valeur de la constante universelle de gravitation G, les masses des particules élémentaires ou la vitesse de la lumière. Il existe des modules qui intègrent des valeurs précises de ces constantes, comme par exemple le module constants faisant partie du module scipy.
from scipy import constants as cst
Dans ce module on trouve par exemple :
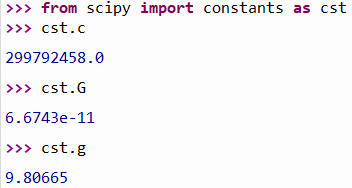
nom_variable_1 = 12 #on place le nombre 12 dans la variable (boîte) nommée nom_variable_1
nom_variable_2 = "texte" #on place le mot 'texte' dans la variable (boîte) nommée nom_variable_2
Pour récupérer le contenu d'une variable on utilise simplement son nom. L'opération suivante permet de multiplier par 2 le contenu de la variable (boîte) nom_variable_1 :
nom_variable_1 * 2 #prend le contenu de la variable nom_variable_1 et le multiplie par 2
Pour afficher un texte, une valeur, un résultat on utilise la fonction print
print("le contenu de la variable est : ", nom_variable_1) #affiche le texte entre guillemets et le contenu de la variable
Pour demander à l'utilisateur de saisir une valeur, on utilise la fonction input("texte") qui renvoie une valeu de type texte à stocker dans une variable
saisie = input("veuillez saisir quelque chose") #stocke la saisie au clavier de l'utilisateur dans la variable saisie
Exercices à réaliser pour appliquer les notions abordées plus haut au format pdf : voir l'énoncé.
(c) Stéphane Jouaire, SNT 2019-2022